Tantalizingly, the images just about meet, coming as it were to very similar or obviously 'same' places only on different paths, from different starting points. Going from the classic Mandelbrot fractal to Julia sets, from the signature rotate and shrink of chaotic systems to the clever diamond square and fm plus Perlin noise cheating shortcuts, there is always seemingly just out of reach - or at least out of *my* reach for now - the common core that is unchanging throughout, the possibly illusory model that finally provides one a full understanding of the matter so that it's clear not only all that can be obtained but also how. Most likely though, it's truly as old wisdom says - at core the whole of it is just Maths and Language, structure and expression. So, setting aside any lofty goals and higher expectations of full understanding, I simply went a bit exploring in the 3d complex space this time - the space with one axis real and two complex (hence, a whole imaginary plane rather than merely an imaginary component). What I found when slicing through to get a 2d section was, quite as expected, the Mandelbrot shape, even if rather lusciously1 coloured in by all three colouring methods I had already implemented for iterated polynomials:
Taking the fractal shortcuts in 3d complex space too didn't take long to implement at all, seeing how it's just a tiny addition to my trusty generator, merely plugging in a different function for the painting part and letting the rest do its job as usual. There's a sort of smudgey style to the colouring overall but otherwise the underlying structure seems to my eye quite reliably, reassuringly bringing together several styles that were before obtained only from futzing around with various parameters - suggesting that this is indeed on the way towards getting the hang of a better, more useful model of the whole. Seeing how it's such a model that I'm after rather than just pretty pictures, taking the time and the exploration to get there is fine with me and on the way, the pictures, beyond providing a possibly haunting collection of eye-like drawings, might also make for interesting Maths illustrations at the very least, I'd say, so here's a small sample:
While I don't really intend to write up this time in much detail the technical parts behind all the above, the very basics are straightforward: a 3d complex number is x*j+y*j^2+z*j^3 where j^3=-1 and zero is a full plane, x-y+z=0. I've taken this description that seems fundamentally correct to me, from Reinko Venema2, who seems to have gone even further on the Maths side to n-dimensional complex numbers. Using this basic definition of 3d complex numbers, I simply naturally extended the rest of notions I needed for the various types of colouring I already had from the usual complex numbers. I'm quite happy with the results obtained so far and everything seems to fit perfectly well indeed so I don't particularly see any need to change any part of it for now.
As to the 3d or even nd complex space itself, there is certainly plenty more to explore, especially on the expression side, since what the "eye" can see so far seems to me to be rather little and possibly way too dry, with only a hint of a glimmer in that Mandelbrot fern part for instance. Not that I ever lacked what to explore, really, so don't wait for me on this if you are interested, simply pick it up instead and take it further. If you do, I'll be even quite curious as to where you get with it, just let me know in the comments below.
Seriously, it actually looks better than you can see here - processing the pics for the web in this instance visibly hurts, taking away apparently the sort of detail that counts and making the pics look rather dull by comparison. Still, I don't feel at all like going again through the pile to pick them and upload them in full, glorious size and this write-up anyway waited for more than a month to get done so you'll either have to take my word for it or regenerate them to see for yourself. ↩
Or so I assume his name to be, as the only place I could find a name on that whole site was in what looks like a test comment. I wanted to leave him a comment or contact him some other way to at least let him know of this tiny related use but I failed to find any contact details as such and I'm not going to go now through all the trouble of making a wordpress account or somehow digging up that 10 years+ old account of mine, if it still exists, just to leave a comment. If any of my readers has a wordpress account at hand and doesn't find it too much trouble to comment there, perhaps there's still a way to reach out and communicate but otherwise it doesn't seem all that likely. ↩
Comments feed: RSS 2.0



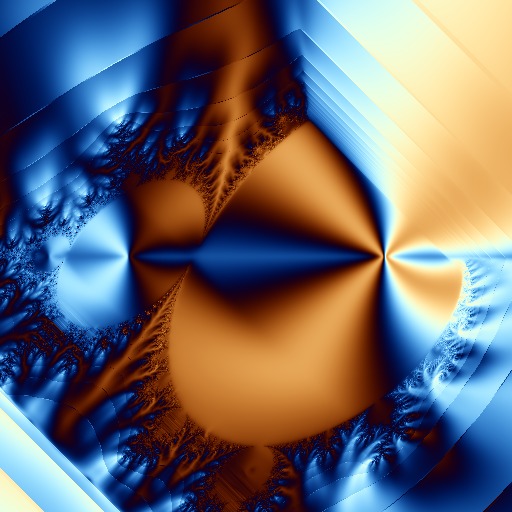










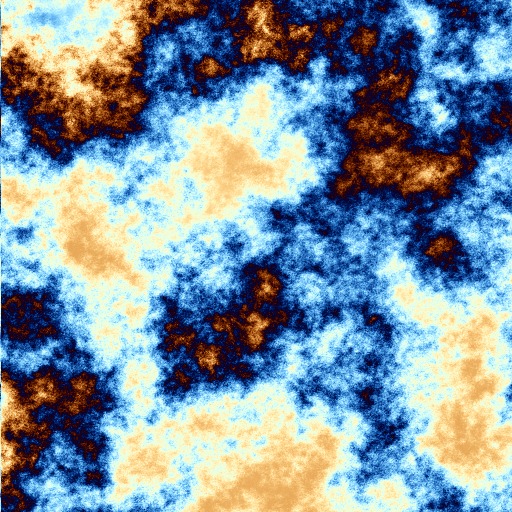



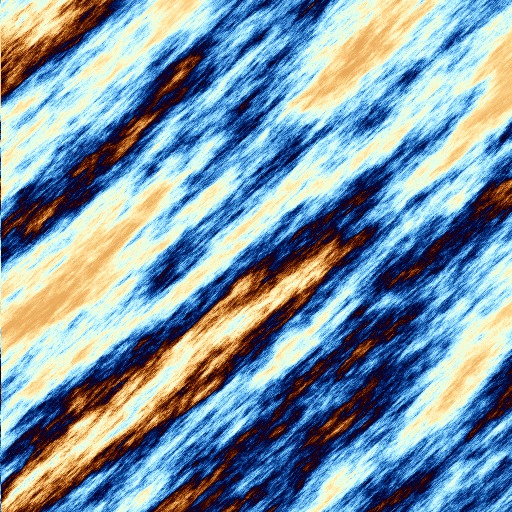

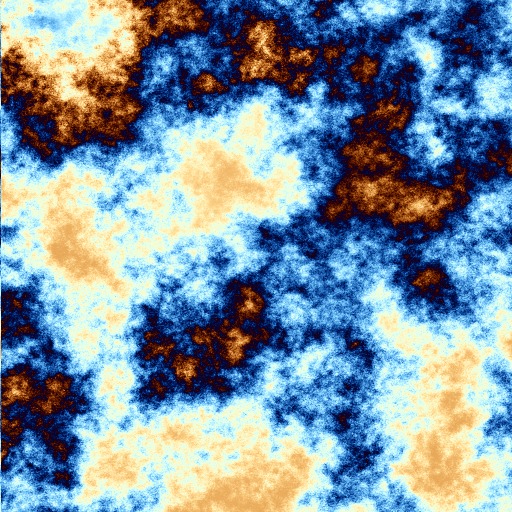
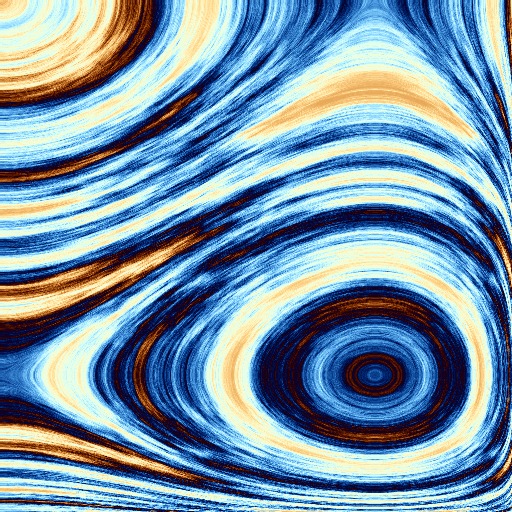
For more pictures going into more than 3 dimensions, too, see next article.
Worth noting that my statement above that "zero is a full plane" is potentially misleading - the numbers in that plane are indeed all divisors of 0 but in this 3d complex space, this does *not* mean that they are all 0. Indeed, there are non-zero divisors of 0 and so the correct description of that plane is exactly that - the plane of divisors of 0. Visually, this is linked to the 'broken fern' effect (and likely most of the 'scattered dust' areas) in the above pictures as they are mostly due to my over-cautious approach to division in this new space where initially I had avoided dividing by any number from that plane although it's of course only the actual zeroes that need to be avoided. I corrected this in the more general implementation done for the next article but this will remain as it is.
[...] earlier first pictures of the 3d complex space were quite encouraging, I took the time to figure out all these additional dimensions a bit better1 [...]