Programming turns inside out the traditional fitting of the square peg in a round hole: in the computers' binary worldview, it's the randomly generated sphere struggling to fit in a deterministic square grid. The rigid limited precision of the digital medium together with the natural pro-patterns bias of the human programmer leave very little space for true roundness and possibly even less for true randomness.
Roundness and randomness in the digital tend to get therefore approximated at best and whether such approximations are good enough or not for you depends, of course, on how closely you look at them and what your needs are. Beware though that randomness is much harder to evaluate than roundness through mere looking and it's also much easier and more likely to get silently lost or at least subtly damaged on the way, even when verifiably provided as input. What may seem at first totally innocent and otherwise perfectly valid choices of implementation can have unintended consequences with respect to actual randomness that makes it through.
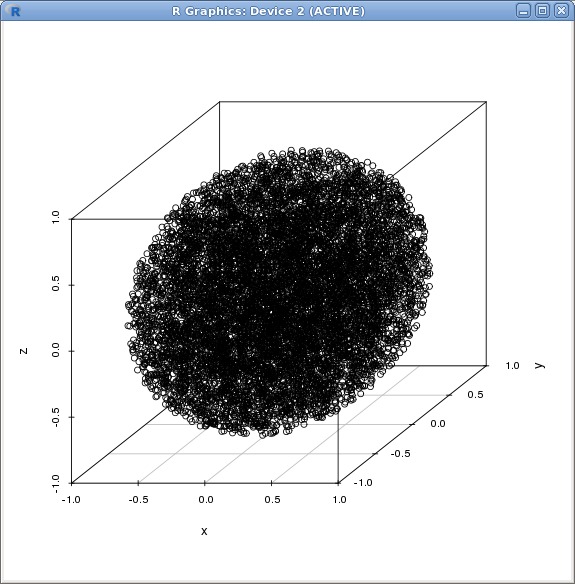
To illustrate the above, consider this seemingly easy task of writing code to pick random points1 from within a sphere centered at the origin and with unit radius. Repeating this for long enough would naturally produce a "noisy" model of a sphere since all points inside the sphere have equal probability of being chosen at every pick. For instance, 10`000 such points might look like this when plotted on a 3D grid:
The randomness-preserving implementation that produced the above set of points is quite simple: request from your reliable random number generator 3 numbers in the interval [-1.0, 1.0] and keep them if the 3D point they describe is within the desired sphere or discard them and try again if it's outside of the sphere2. Since the interval given covers the 3D space of a cube (as imposed by the square grid) rather than a sphere (as desired), it obviously follows that some of the points will be outside of the sphere but how many might that be? The cube's volume is 2*2*2=8 units, while the sphere's volume is 4*Pi*1/3 ~= 4.19 units, so the probability of a point being *inside* the sphere is only slightly better than half or, more precisely, 4.19/8 ~= 0.52. Conversely, the probability of a point being outside the sphere is (8-4.19)/8 ~= 0.48. Hence, on average, the code will simply discard 48% of the values it requests from the random number generator.
The apparent wastefulness of the above solution (discarding almost half of all inputs!) is so counter-intuitive or possibly even irksome that it naturally invites "corrections" and "improvements" almost instantly. It's not *just* the size of the apparent waste but also the fact that it's so shamelessly obvious and with such clever solutions readily at hand to avoid it that it's almost as if made on purpose to... tempt. Which is quite fitting after all, since what would von Neumann's state of sin3 be really worth if there wasn't any temptation to lead one to it?
As with all other temptations, the only protection that ever works against it is well-rounded experience. Where the inexperienced will rush directly to "improving" the implementation, the more experienced will take the time to at least explore in more detail the alternatives and with a look towards finding the reason why they were not chosen in the first place rather than finding just why they would be so much better than the choice made. Even so, the conclusions drawn from such investigation still depend on how close one looks at the data and, perhaps, simply on one's outlook to start with, as well. Looking to find something can all too easily get in the way of fully seeing what one is looking at and not even experience is always enough to help one with this sort of trouble.
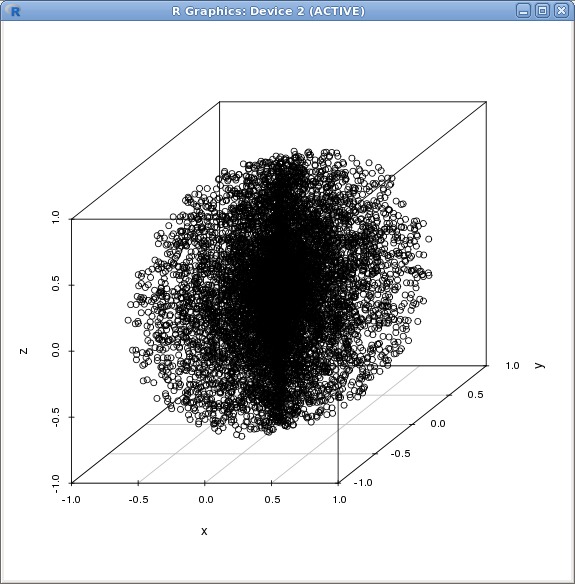
To illustrate though, let's have a look at some concrete alternative implementations and what they yield. One straightforward approach is to use polar coordinates for describing the points in the sphere and interpret the three random inputs as two angles and one distance from the centre. The result of this makes it quite obvious that there is some damage done to randomness, given the noticeable pattern that appears:
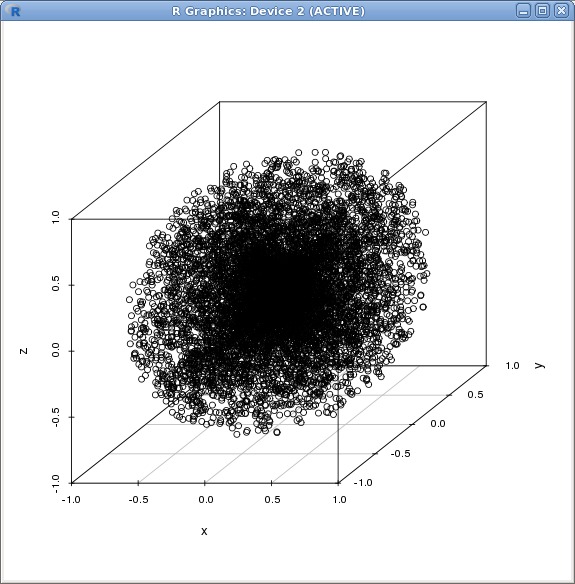
Another approach is to use vectors for describing the points in the sphere and consider 4 random inputs for each point, with 3 giving the direction (normalising the vector) and the 4th the size. The straightforward corresponding implementation of this shows once again a noticeable focus on the centre of the sphere:
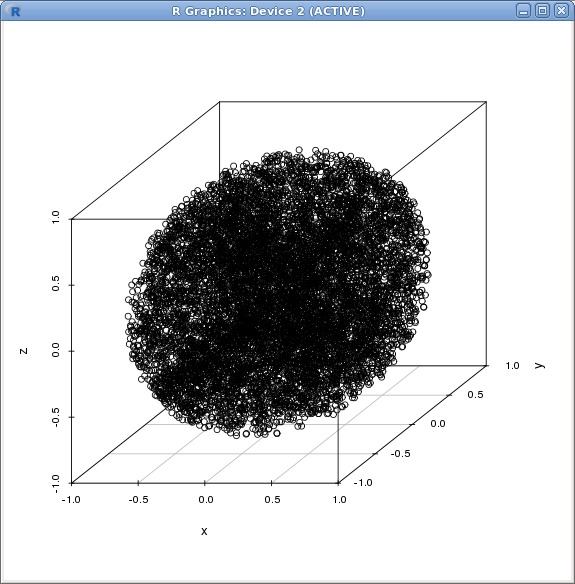
When the aim is to make the loss of randomness simply less obvious, the above approaches can be further refined, aiming essentially to correct the observed damage regarding the way the resulting points are spread in space. Generally the correction would apply some transformation to bring the resulted coordinates of points (back on) to a normal distribution. For example, using the cubed root as multiplier for the size of the vector in the 2nd approach above does spread the points better away from the centre indeed (although some subtle pattern is still visible to my eye in this plot compared to the very first image):
While there certainly are other alternative approaches possible, the reason why I am not aiming for a more systematic overview of them is that the trouble is more fundamental: all the attempts to "improve" on the very first implementation boil down to introducing another layer of deterministic computations between the values obtained from the random generator and their use. In other words, they *reduce* the randomness at best, even though they can indeed be made otherwise to maintain for instance a normal distribution of the obtained points, hence the appearances at least as far as data plots are concerned.
Discarding randomness to avoid discarding instead 48% of the input may seem like an improvement only if randomness wasn't all that important to your use case in the first place. Quite often, this is even the case, since the more common goal is to simply approximate randomness well enough for human perception and that is a relatively low bar where randomness is concerned4. Just make the tradeoff very visible, don't confuse pseudo-randomness with randomness and be very wary indeed of improvements that might have more subtle effects than intended or perhaps simply more than you can notice from merely looking at a sample output or even checking that it follows some expected distribution.
I'll assume throughout this article that such random points have an underlying normal distribution. ↩
This is the very simple golden standard of preserving randomness really: use the inputs as given, discard and try again if they are not fit for purpose, nothing more. ↩
"Anyone who attempts to generate random numbers by deterministic means is, of course, living in a state of sin." ↩
This is actually what even triggered this article - I've been working some more on various graphics, resource distributions and similars, basically on an upgraded scope of that older task of finding useful mixtures of order and chaos for all sorts of fun. ↩
Comments feed: RSS 2.0