The idea behind the Diamond Square method (DS) is deceptively simple: take a set of pseudo-random values and keep mixing (averaging) those on symmetrical positions, storing the result of the mixing at the symmetry centre, while decreasing and rotating the reference frame at each iteration. In the two dimensional case that is most commonly used in computer graphics, the reference frame is basically a square that gets called a "diamond" when rotated 45 degrees, hence the DS name. For the first step, the frame is square and as big as the whole image: the values in the 4 corners are therefore averaged and the result is added to the value in the very centre. Then, the frame is rotated 45 degrees (hence, the "diamond" part of the step) and used again to average the new corner values and add them on top of the new centre value. At each subsequent step, the size of the frame is halved and then it gets again applied both as a "square" and as a "diamond", basically mixing together values on increasingly closer positions to one another - in other words and from a graphical point of view, adding (in the sense of making noticeable patterns out of) more and more detail.
The above method (average corners and add to centre, rotate and do the same, then halve the size and repeat it all) can be applied to any number of dimensions really but there's a whole lot that this apparent simplicity packs even in 2 dimensions so that there's no need just yet to add even more dimensions to the mix. Before going though into any further discussion, one might reasonably ask: does it work? Well, it's a lie indeed but a very effective lie - at least in knowledgeable hands, so whether it works or not depends on the skill of the one using it. More precisely, in the computer graphics context, whether DS "works" or not depends mainly on the inputs it works on (the range of those pseudo-random numbers) and the way the outputs are interpreted (the colouring scheme). To illustrate, here's for instance the very same DS method, with the very same parameters of size and starting step, only with different intervals chosen for the pseudo-random numbers so that the "grid" of the method is clear in one case and rather invisible in the other:
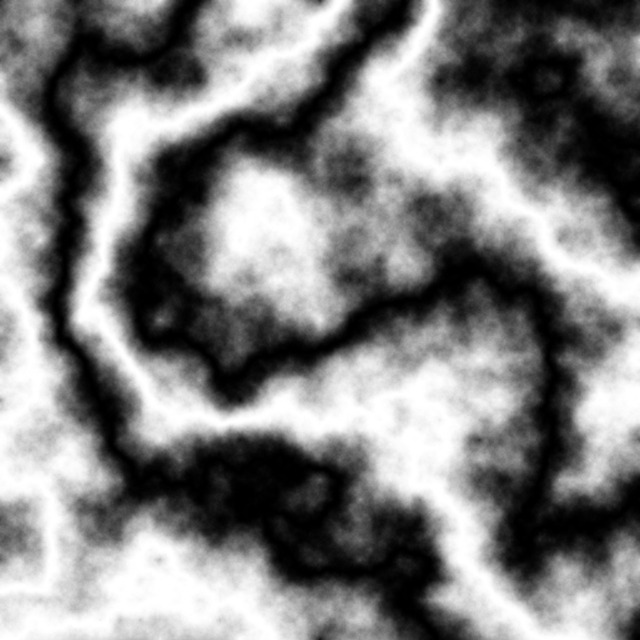
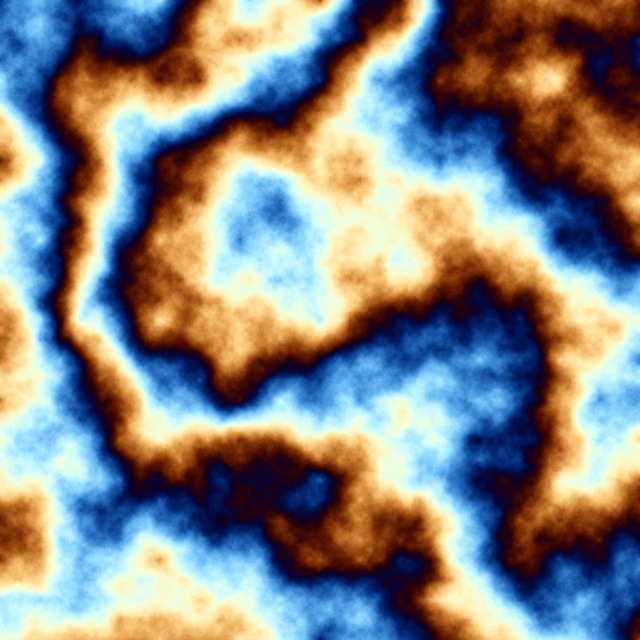
The above illustrations are grayscale for the simple reason that DS tends to be used most commonly to generate heightmaps, where the value at each pixel stands for the height of the terrain at that point, hence a single value. This doesn't mean however that DS can't lie convincingly in colour, quite on the contrary, have a look at the same DS results as above, only using an r,g,b colouring scheme as opposed to the grayscale one:
Note also that the DS method does not necessarily require that one always starts with a frame as big as the whole image or that one always goes all the way to the tiniest detail. To illustrate one side of this at least, here's a series of images showing the result of DS for different starting sizes of the frame, both in grayscale and in colour (the smaller the starting size, the more "packed" the image - basically the smaller the size of the patterns or "features" that appear, since the correlations are made between closer points):
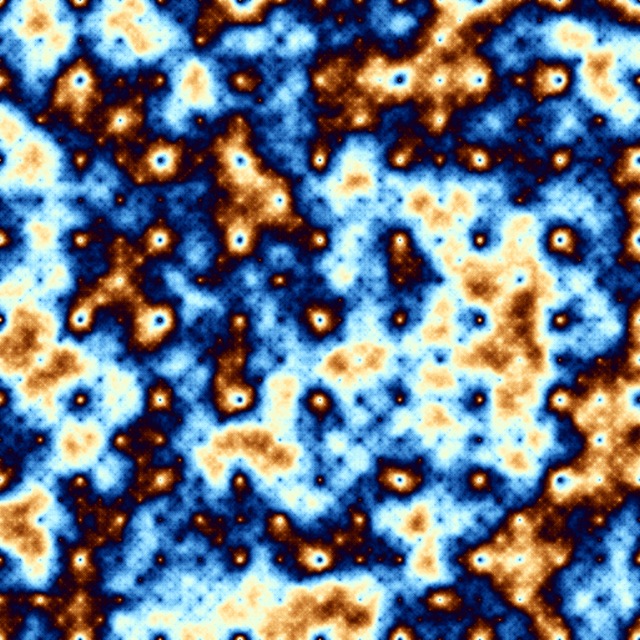
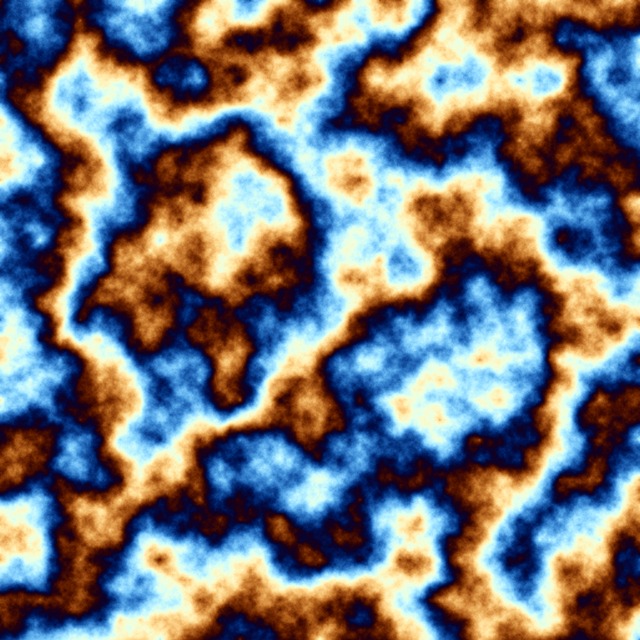
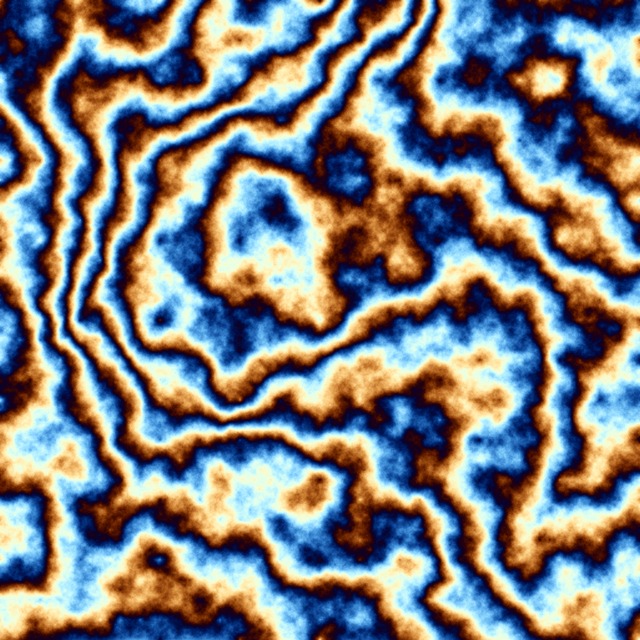
Does the above mean though that smaller features can only be obtained through DS at the expense of less correlation between more distant points? Well, there's more than one way to tell the same lie for sure, so if you want more detail while still keeping the higher level correlations, simply pick a suitable colouring scheme (to cycle well) and then increase or decrease the range of those pseudo-random values so that... they each matter visually more. Then you can even keep to the standard DS that starts with a frame as big as the whole image (hence maintaining ALL the levels of correlation within the final image) and then pick wider or narrower range for the pseudo-random values, depending on whether you want smaller or larger features visible in the final image. For illustration, here's a series of the very same DS applied in turn on values in the range -1.0 to 1.0, -2.0 to 2.0, -5.0 to 5.0 and -10.0 to 10.0, first in grayscale, than in full colour:
While the images above can help perhaps each reader answer for themselves that basic question of whether DS "works" or not, depending on what they want out of it anyway, there's a bit more to be said about why does it work the way it does, in the first place. How can it even be that such a simple and rigid, grid-based method can generate nonetheless images that are - if anything - less obviously grid-like than some generated for instance with the fbm and trigonometric distortions of the input domain?
Your own answer to the above might be different from mine and if it is, I'd be quite curious to hear it so write it down in that comments box below this article. The way I see it though, this patterned but not rigidly grid-like result of an otherwise strictly rectangular and grid-based method is not that surprising, since DS seems to me to be a very smart simplification (in that it picks out of a lot of complexity the very core that matters most for the task at hand) of a chaotic system, nothing less. After all, look at that application of a square frame and note that its rotation and then halving (hence: contraction) is precisely the sort of iteration required by an IFS (iterated functions system) to ensure a unique attractor. So yes, the chaos got trimmed to the bare minimum perhaps, what with the fixed square shape, the pseudo-random numbers and the very limited number of steps for fully calculating each image (each point in the image really is calculated in fact only once - at least unless you insist to basically iterate the DS itself, as well). Nevertheless, it turns out that a drop - a well-chosen drop - of chaos is quite enough for the screen to lie quite convincingly or at least convincingly enough for the human eye.
Comments feed: RSS 2.0













My philosophical explanation revolves around the (fundamental!) notion of hierarchy.
Because there's an unyiedingly rigid hierarchy (expressed in the relative importance of points as implemented through the halving -- most points give least of the effect and an elite most of it) even the most banal random dispersion coalesces into art, souls and all the rest of fundamentally human expression. It's all it takes, really, to have people : rigid hierarchy. Nor can there be such a thing of people without it. Importantly, the rigidity needn't come from some association with specific points ; what's contemplated are merely the proportions.
I think that's at best perhaps a necessary part of it but not quite sufficient - picking for instance simply n points and inflating their values *individually* ie unrelated to one another, won't do anything other than some blots in there, not quite sure if that qualifies for much of that fundamentally human expression.
Through the DS algorithm, there is a "hierarchy" indeed (since at each step the weight is halved as well, not only the size of the frame) but the effects of the points on any specific level in this "hierarchy" are correlated and moreover there is further correlation even between the change in magnitude of effects on different levels. Basically there's some inner structure within each level itself and there is further structure in how the efforts of different levels combine, too.
As to the lines in the last image: what I did in the last 4 images was to increase the interval of the MT values used to seed the whole thing. This in turn and with your "hierarchy" notion above forces essentially... more inequality. The last image is seeded with values in [-10,10] while the one right before it is seeded with values in [-5,5]. This being said, there's more to the whole thing since the final image you get to see further depends on the colouring schema chosen - both the grayscale and the colour images use a trig-based (cos) schema and that adds further its own specific type of (rigid) structure.
[...] fractal to Julia sets, from the signature rotate and shrink of chaotic systems to the clever diamond square and fm plus Perlin noise cheating shortcuts, there is always seemingly just out of reach - or at [...]