For the past week, Eulora's latest version of client and server have been communicating with one another happily and uninterruptedly - as well as actually RSA-authenticatedly and Serpent-encryptedly, generating, exchanging and automatically burning keys as needed, creating accounts, exchanging IPs and generally doing everything as required, not to mention being able to recover from all sorts of troubles, errors as well as any other difficult & unexpected situations that the hell otherwise known as "testing setup" throws at them. So I watched them for a while - there is some beauty to working things going on about their job and handling it all without skipping a beat - and then I switched to just keeping an eye on them, checking logs, sampling measurements from time to time and generally taking notes for future minor and less minor further improvements that are perhaps possible. As useful as all that is though, there's hardly anything in it to keep me busy for hours, let alone for days. So I rebalanced by getting back to the graphics pipeline that was patiently waiting for me to pick it up again.
The step taken this time on the graphics side covered the implementation in Ada of the polygonization of an implicit surface - where "surface" is a very loose term, covering anything at all, as long as it's given through a function able to return positive, negative or zero at any point, corresponding to some convention as to whether that point is to be considered outside, inside or exactly on the surface of interest 1. In the overall graphics pipeline, this polygonization of a surface is a mandatory step for obtaining a mesh that CS/Cal3d can work with - such a mesh is needed both for moving objects 2 and for non-moving objects of any sort that might be found somewhere in Eulora.
At the previous prototype stage, I had relied on a C implementation of Bloomenthal's algorithm for polygonization of implicit surfaces using essentially a 3D lattice of cubes to gradually explore all the space where the surface might be. While the C implementation is quite neat and has certainly been useful during the prototyping stage, it is quite tightly packed indeed 3, so that clarity is not exactly its plus and it also has some limitations (most notably on the total number of vertices due to the hashes and hashmaps it defines and uses, as well as overall on the size and level of detail of shapes it can handle, since it caches most of the data and this means that it runs out of memory on too large or too detailed shapes). Moreover, there's nothing like implementing an algorithm to *fully* get to know it in detail, especially from a practical (as opposed to merely theoretical) point of view. Finally, I should probably also add that I'd very much prefer to have the full pipeline in Ada rather than keep mixing languages at all steps, so I had to implement this part as well anyway.
The translation of code from C to Ada is not all that straightforward even if one attempts as a first step to do just a pedestrian copy - there are simply structures and approaches that don't have direct equivalent or are plainly illegal in one language while being the very core of implementation in the other. This was very clear from the very start so I didn't even try that, but I went instead through the original C code very slowly, with pen and paper in hand, figured out all the pointer gymnastics, bit diddling artifices (C-style, it is what it is), global variables, intricate data structures and their various roles as well as the exact way in which they end up linking to one another (there are linked lists, of course, but also multi-dimensional lattices and lists of lists - quite standard fare for C programming, exactly as I recall it from all those years back even though it took a while to get back into that frame of mind). Gradually, I could find the seams on which to cut the whole into parts and then I could as well start implementing it step by step (as opposed to trying to do it all in one go so that there wouldn't even be any way to know what or where the trouble was, if it failed.
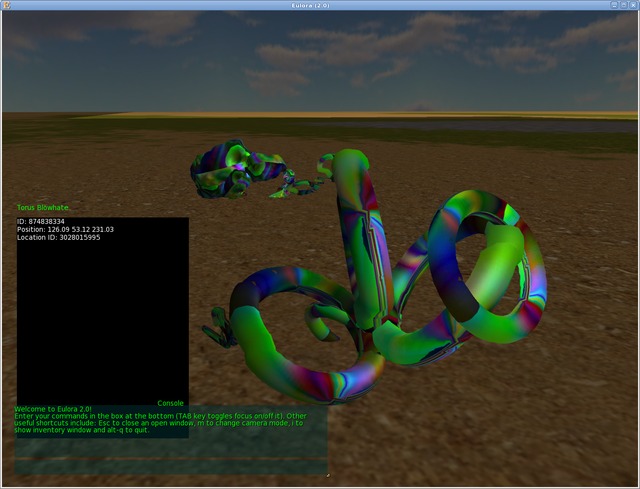
A few parts of the new implementation could be directly tested against the output from the original C implementation. Most notably in this category, the cube table storing all possible polarities of a cube and their corresponding resulting polygons. For those parts, I instrumented the C code to produce some reference output and then used that to write a test that captures thus exactly what the result should be. But the trouble with polygonization of surfaces (and possibly graphics, more generally) is that there isn't a single "correct" solution for most tasks - so one can't really compare results in such a direct way. Moreover, since floating point calculations are significantly involved at all steps and the 2 programs use different prngs, it's quite guaranteed that the vertices obtained will *not* be the very same - so comparing the list of vertices and even that of triangles is pointless. The more important part is whether the result does cover indeed the intended surface and whether the output fits as expected within the existing pipeline afterwards. So to check this part, I used first a simple surface - the torus, undeformed by anything - and otherwise directly inserted the plain text output of my Ada-polygonizer into the rest of the existing pipeline, basically handing it over as input to generate the exact xmls for mesh, cal3d mesh, then model and fitting animation. All went swimmingly, the model was created and packed, then the file chunked and indexed, the character created for my test player and as a result - meet the pc of many tori, otherwise known as Blowhate, Torus Blowhate:
As you can see in the picture above, so far the shape is undistorted (not to mention not at all the usual mesh that I use otherwise for creating hopefuls). The apparent distortion of the torus is due to the animation really - it bends the uncooperative shape at a weird angle. Nevertheless, the relevant part for me at this stage was that the polygonizer actually produces a torus as opposed to whatever else and that its output has been successfully consumed otherwise by the formatter and the rest of the pipeline. The next step will be to write in Ada the parts producing also all the required formats directly and then bring back the more interesting shapes, port to Ada the rest of the pipeline as well and finally integrate it all so that it provides any required graphics whenever needed.
On a side note from all the fun above and since I have this occasion to compare the two languages in some concrete situation, I can add that the whole of "Ada is very verbose while C is oh so very compact" doesn't turn out to be all that true in practice: the original C code has 808 lines (even after discarding some parts that were really not needed such as the display on a SGI workstation), while my current Ada polygonizer has 934 lines (.ads + .adb files) and I didn't try in any way to make it compact (ie, there still are plenty of comments too and I'm sure that even the code itself can be made more compact if aiming for that). What I can say on this is that the C code spends a lot of lines on defining and allocating/deallocating memory for all those intricate data structures that it uses for caching some data (not even all data, though). Given that my Ada implementation does *not* cache the intermediate data at all so far, there are way fewer new definitions for data structures to start with. There are still some allocations for the final data but those use predefined data structures.
From a practical point of view, the current Ada implementation still requires a few iterations that will be best informed by use, as soon as I get the full gfx pipeline implemented in Ada and so I can put it to some serious use. For now, it handled happily situations that the C code could not handle (e.g. not choking on "too large" shapes, nor balking just as easily on "could not find starting point") but it is true that all that re-calculating of surface values every time can increase the run time when the number of visited cubes is high enough 4. Nevertheless, so far at least, it didn't really matter for the the sort of meshes I needed to polygonize - if it turns out that it does matter though, I'll update the implementation to cache the values one way or another, it's certainly perfectly doable in Ada just as well although without all the lists of lists necessarily.
- The inside vs outside distinction is important in computer graphics because of how the lighting models work.[↩]
- PCs aka player characters and NPCs aka non-player characters.[↩]
- Note that I'm using the direct cube-based polygonization as opposed to the tetrahedral-based variation that he includes as well. The tetrahedral-based variation first splits each cube into tetrahedra and then polygonizes those as it's a simpler task - the whole implementation is therefore in principle shorter and easier to follow but it results in even more vertices and triangles for the same surface. When used for Eulora's purposes, all those additional vertices and triangles take up space and basically cost to be processed, stored and then sent over to the client at the very least, while not necessarily making otherwise a huge difference to how the mesh looks on screen (since more detail is not always actually an improvement). So I kept at least for now to the polygonization that gives the most compact *result* even if it requires perhaps a more complex implementation. After all, the implementation is done only once.[↩]
- For a concrete data point here: the Torus shown in the screenshot is generated with a cube width set at 0.05 and a maximum number of cubes in each direction set at 40 (this makes for 81*81*81 total maximum of visited cubes). The Ada implementation took 0.08 seconds on average to do it, while the C implementation took 0.02 on average.[↩]
Comments feed: RSS 2.0