~ This is a mixed up article with serious pictures for easy reading and silly text for hard staring. ~
Following last week's discovery of the missing link in CS's capabilities (no meshing and no tesselation implemented as such), I took another dive in the ocean of words on the matter, reviewing papers and theses and software monstrosities by the boatfull1. At any rate, the core ideas are very few indeed: the focus is almost exclusively on either "assisting the artists" (in that dumb sense of catering to their convenience rather than to any attempt at excellency or even plain exploitation of the possibilities of what is a different environment than that of the traditional drawing/sculpting) or otherwise reconstructing surfaces from a *lot* of data that comes from scanning objects so basically yet another facet of that great new definition of success as approximating unanalyzed data.
The algorithms are mainly variations on delauney/voronoi refinement, marching cubes/triangles/particles for surface reconstruction and otherwise the whole of bones and skeletons pretty much stem anyway from Blum's medial axis - that is indeed the topological skeleton of a shape but is also precise enough to result in practice in a lot of small bones if it's taken as such. As it tends to happen in the best of cases, when I was just about to run out of oxygen for good on this, I finally turned out instead something quite promising and much in the same way as before - among the dull and broken "let's tweak this to change that", something glimmered all of a sudden, in quite the same way as Blum's earlier beautiful paper on the medial axis - this time it was Bloomenthal's paper2 that went straight and unapologetically to the heart of the matter, from the very first sentence: "An algorithm for the polygonization of implicit surfaces is described and an implementation in C is provided." And wonder of wonders, what this amazing first sentence promises, the following words actually deliver, too!
The algorithm itself is just about as simple as one can make it for the task at hand: the core idea is to use cubes of equal sizes for partitioning the space, to gradually build such partitioning through step by step expansion from a starting point on the surface until the whole surface3 is contained in the obtained collection of cubes and then to decompose each relevant cube's face into the corresponding polygons (triangles for my use). The directions to expand to at each step are easily identified by considering the sign of the implicit surface function at the corners of each face of a cube. And taking advantage of the regularity of equal-sized cubes as partitioning cells, the different cases and their corresponding meaningful expansion can be precomputed and then simply used. Note that in all of this, the cube's size is indeed fixed but it's a parameter of the algorithm - basically larger cubes provide less detail and that has the advantage of fewer vertices and corresponding triangles but also less smooth resulting faces/shapes that can run into very poor approximations of the actual surface especially where it curves.
In 4 neat pages, the paper goes through a clear description of the method, a discussion of some implementation choices for simplicity, flexibility (e.g. the intentionally black-box approach to the implicit function definition at polygonization time so that one can use a continuous function as intended but also anything else really, as long as it accepts a set of 3 real numbers and provides a positive/zero/negative result) and speed (in particular the hashing of values -such as vertices- that are re-used during the building of the collection of cubes containing the whole surface), several concrete examples of some implicit functions (a torus, a jack, a blob, a combination of two tori) and a brief discussion of potential issues (especially if the implicit surface function is not C1 continuous since in this case various artefacts may appear, such as truncated edges or jutting parts).
The promised code is indeed included - if in a horrible form since it's literally dumped in a .pdf at the end, the stuff of horrors as far as code is concerned. Nevertheless, it is *plain C* indeed, it is less than 1000 lines in *total*, even including some examples and whatnots, it is clear, commented, properly named and everything else that requires apparently rediscovery nowadays and it was not even mentioned as anything special back in the 90s. Anyways, I read it at first half-expecting it'll turn out to be just a "proof of concept that kinda maybe works on narrowly chosen examples". As I read, I started to realise that it might actually be for once, something useful. And then I went ahead and picked the parts that I need, wrote them down in a .c file, compiled the whole thing (imagine this, *nothing* required other than a c compiler, ok?) and then started playing around with it. Ah, the joy, the pure and proper joy of *finally* having something to play around with rather than suffer through, for once.
Despite all the wonders above, the implementation as it stands has its own limitations - although at the moment I'm not even sure if those limitations are not in fact quite useful. The most important one is that a run can fail in 2 cases: if the starting point is not close enough to the surface or if the polygonization runs out of allocated memory for the hash tables it creates.
The first trouble is a bit of the price paid for the simplicity of the algorithm: the first cube built around the starting point has to include some of the surface or there's no way for the algorithm to know which way to expand to discover the rest. I don't think this is much of an issue since yeah, I plan to build my implicit surface functions so that I can at least find ONE bloody point on the surface, one way or another4.
The second trouble related to running out of allocated memory can in principle be addressed most easily by expanding the maximum allocated memory (though this may be a bit more involved than simply changing a number given as it's not directly exposed as a parameter/variable as such but set within the type definitions and so a change requires careful follow up of all parts that may require change subsequently). Nevertheless, I won't hurry to do this change because it *also* means that the resulting polygonization will have therefore *more* vertices and triangles. And in turn, it's not all that clear that I need or even want more vertices and triangles anyway (and certainly not an infinite/practically uncapped number of them, wtf). So it stays as it is for now, I'd say.
Armed with a working polygonizer, I then looked at the eternal problem of matching the output format of one part (the polygonizer in this case) to the input format of the next part (the client ultimately but possibly the viewer of test meshes first). As the starting point for this was to generate characters, the format needed would logically be the cal3d mesh format since each part of a character in the client would have to be in the end exactly that, a mesh in cal3d format including the "influences" of those bones-that-are-not-quite-bones. Except of course, at this stage there's no fucking influence anyway because I'm just generating the mesh, not the animation and so the "bone" is at best an entirely abstract and rather optional idea, especially while still just trying out the algorithm and the whole. So yeah, I wrote a few lines of awk5 to just do *both* the cs and the cal3d "mesh" format out of the polygonizer's output - not like it's much bother anyway and look at that, I can further *also* do any size adjustment on the mesh at the same time, if I want to (and I do want to, for a reason I hadn't realised at first).
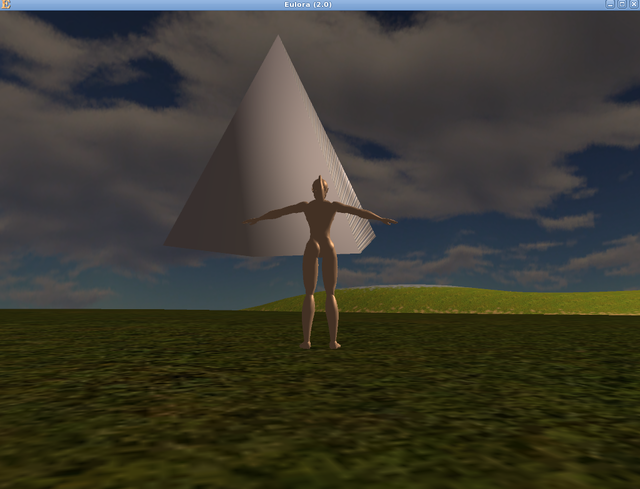
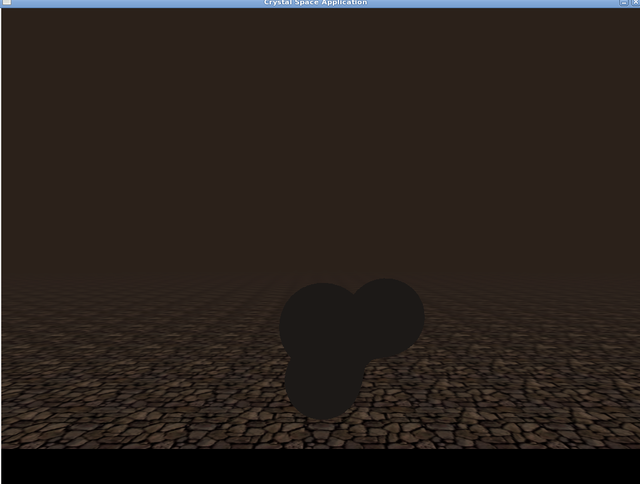
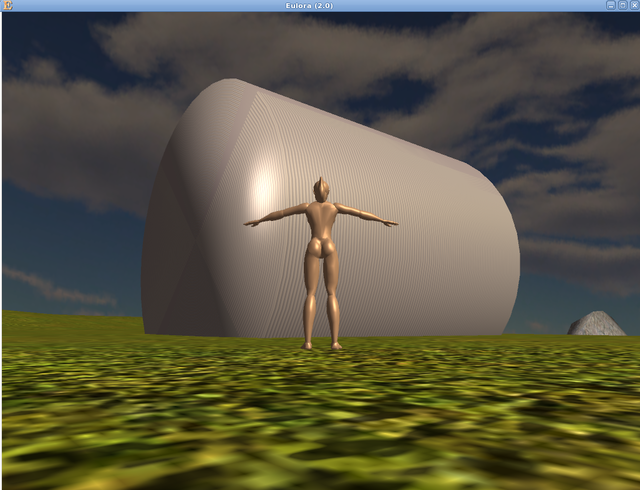
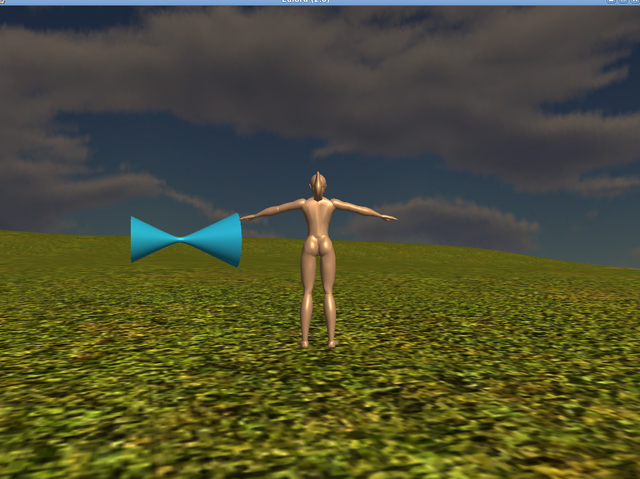
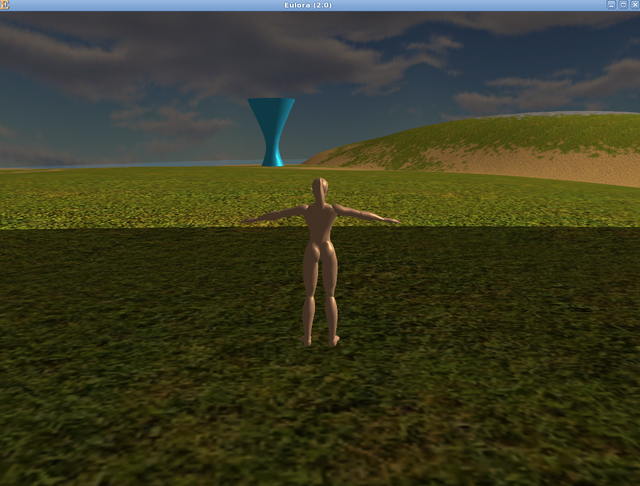
The reason why I did both cal3d and cs format is that visualising just one mesh is in fact more straightforward as such rather than as part of a full cal3d model. And in turn, the cal3d format requires all those bells and whistles that are in fact just stored further calculations meant to support the animation, nothing to do with the shape itself. So let that wait until I have *what* to animate and let's see some pics already. First of all and for comparison with the results of my polygonizer, here's some primitives generated with CS's own internal code that simply has a fixed recipe for a few regular shapes, of which you can admire below what should be a cone (looks more like a pyramid to me, due to how the texture got applied to it), a cylinder (seen directly in the client, through Cally's eyes of sort) and a small ellipse (seen in the viewer). Note that CS itself complains about "degenerate faces" on the cone - in practical terms this means that the collision detection system is likely to have some amount of trouble when that object is involved:
Moving on to something more interesting, here's a collection of various experiments with the polygonizer and implicit surfaces. For starters, here's how a botched torus looks like - I had messed up the equation of the function and so there you go, have some funky wedges, why not:
And here's a blob (made out by combining in the same equation the 3 parts because such are the wonders of Mathematics, yes, you can do what you want, with just an equation, how wonderful) in the extended, cvasi-infinite viewer (I had gotten fed up with the tiny stone cell and moreover, I hadn't yet figured out that the lights were all of a sudden all wrong and as a result making everything that brownish tinge, texture be darned; sigh):
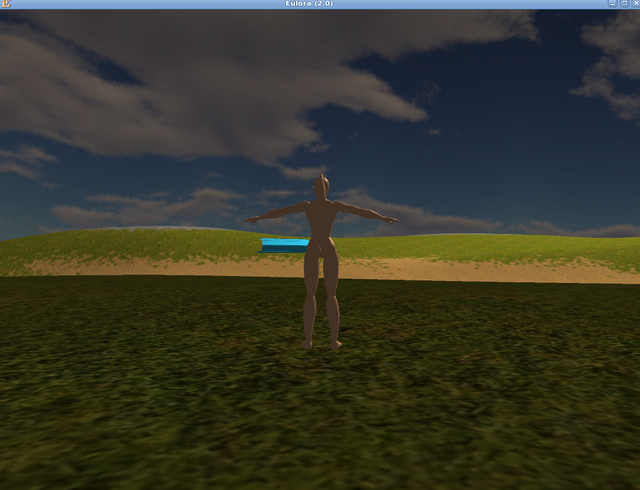
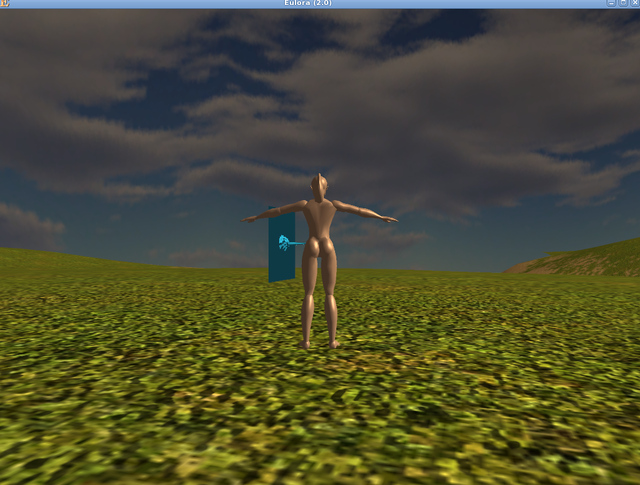
Next on the list and placed in the more familiar landscape of Eulora, a shiny swimming aidtorus6 (the texture is that of some water and it was part of my attempts to figure out the textures too - that is still ongoing because of course it's not quite working as expected, grrr). The weird handle on this torus is a bit...weird. Basically the origin of the torus seems to be considered on the surface for some reason. It's not a big deal, in that it can be easily fixed, of course, but since it's not exactly tori that are going to make a character, I didn't bother all that much to track down the full backstory of how this particular wedge here happened - just be aware that yes, it can happen:

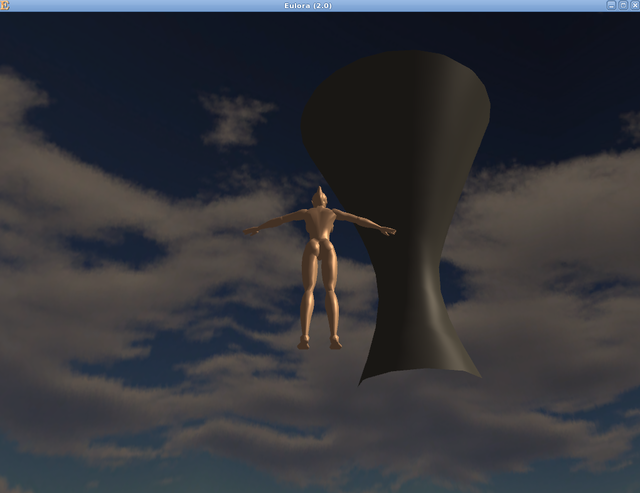
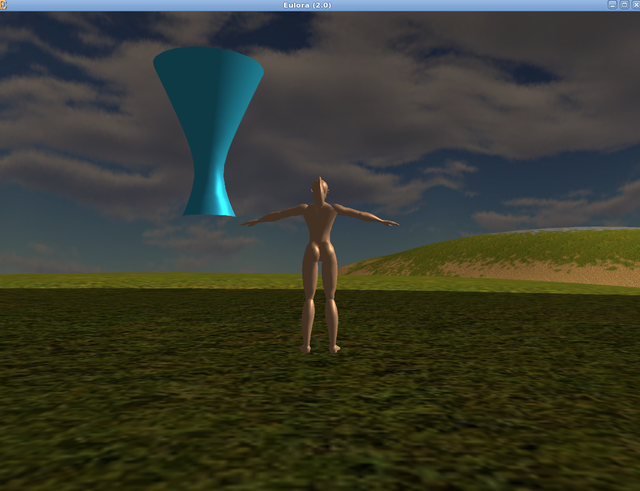
Since after a while even a torus is quite boring, I decided to see how the polygonizer behaves on an unbounded surface - especially since there were no examples of such things in the original paper. One short equation (and a few adjustments to finally streamline my process so that all it takes from generate to view is running 2 scripts & starting the client), I admired hyperboloids of all sorts (and of course they remind me of petroleum refineries, what else):
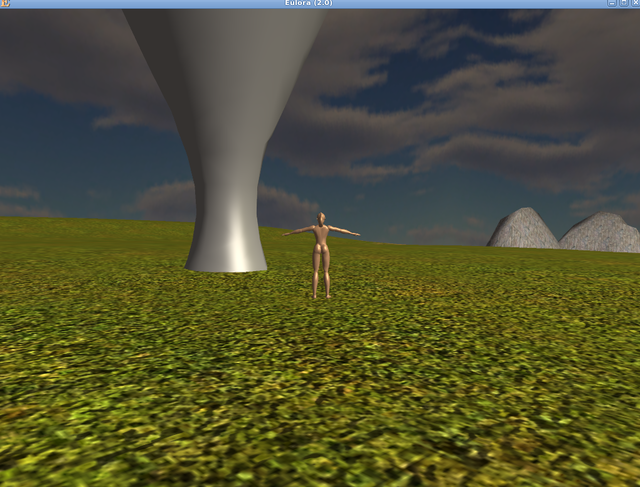
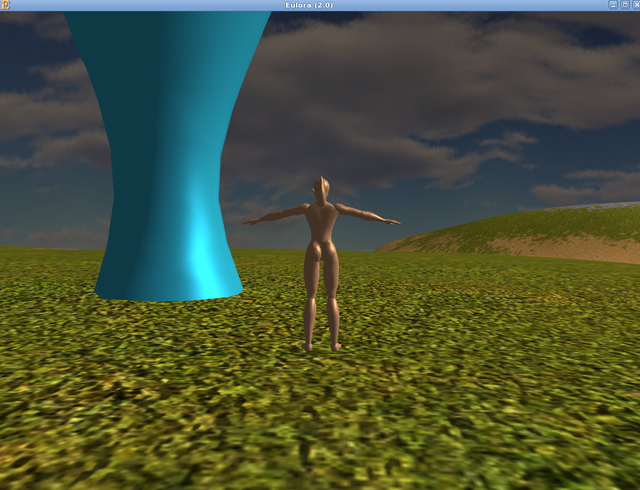
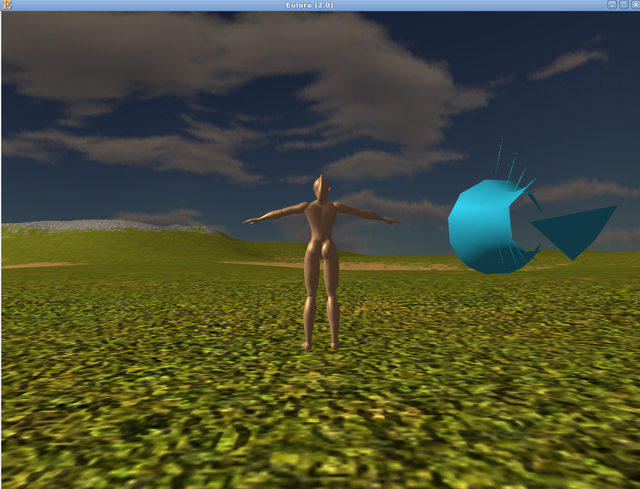
Probably you are wondering now what happened exactly in the last picture and what are those seeming spikes - is that even still a hyperboloid at all? Allow me therefore to assure you that it is indeed still a hyperboloid, no matter what your eyes may tell you. Moreover, it's just as much a hyperboloid as the previous ones were - it turns out however that CS tends to have trouble with the hollow, thin and unbounded surfaces that I generate. When seen from some angles, they vanish entirely and I suspect the trouble is that CS expects in fact two "layers" of triangles to be able to show such a surface as expected - while my polygonizer provides the outer surface of the thing, it does not add to it an inner surface so the "inside" is ...invisible. Is this a problem worth addressing right now? I'd say it can wait for now, even though indeed, look at what mess it makes of what is effectively the simplest "wrap" around an imaginary line-"bone" aka a ...cylinder (if defined implicitly, of course), what:
The above experiment with unbounded shapes set my mind to rest that yes, indeed, the polygonizer can handle those. It also revealed more clearly the need to tweak both the two parameters of the polygonization depending on the shape (ie the size of the cubes and the maximum number of cubes to explore on each side) and the size of the shape after this step. This is because the *size* of the resulting shape depends on those two parameters too. And in turn, the *part* of the shape obtained will depend on them so basically one might need to tweak more than it seems at an initial naive look. Nevertheless, those are very easy tweaks really and at least so far I don't quite see much trouble with them: I've already changed the code to just accept as parameters the two parameters for the polygonization so I don't have to recompile it every time those change; and the script porting the stuff to cs & cal3d gets its own parameter to apply a scale factor as desired so that the *resulting* mesh is exactly the desired size; put together, this means that I can in fact create meshes as big as it might be required to capture nicely whatever details and *then* I can painlessly shrink them too, without loss - obviously, within some reasonable limits since if I shrink everything to a single point, there is arguably some loss of detail, indeed!
As for some fun I had after sorting out all the above, here's a very pointy implement for all your impaling-in-walls needs! It's defined of course through it's implicit function or in other words, you can certainly impale yourself in an equation, no trouble:
The next step on this is to sort out the textures already: the trouble being again a bit of a missing link since CS expects that the texture is an image file rather than an equation/function. I explored already to some extent what I could do there - theoretically there's a way to "write" the texture at run-time ie directly into the render buffer of the thing. But all experiments and even CS's example on this worked in the sense that yes, I can write whatever I want directly to the screen - unfortunately, directly using the screen's own coordinates too rather than the object's coordinates, which is rather a pain (and doesn't quite make sense if I'm supposedly writing to the object's buffer as opposed to a *global* buffer, wtf?). Alternatively, I found also that CS conveniently has even a way to write a texture to an image file but then of course, I don't know how to write & especially how to map such a file to the vertices of a generated surface so that it's neither just a stretched thing nor a tiled thing - the way the mapping of the texture works exactly is quite a pain to fully get because the "explanation" is not helping me much with understanding the approach itself, sigh. Nevertheless, I expect I *have to* figure this out and quite in detail at that, sticking textures for the win and all that. And then of course, I'll need to do and stick the Mandelbrot, yes.
Once the above is sorted, I guess the next thing would be to write the surface function a bit more interesting than the above, generate it for more than one bone too and then - the UGLY part - do also all the precalculations and futzing about that the cal3d format requires in order to put the shapes at the right place, sigh.
I expect the above will still take some significant time, there doesn't seem to ever be a very fast route for what I need to do - or not one that I can yet see.
I won't name all of them, nor even spend more time to do the full write-up, at least not for now. It's not that I can't find what to say or that I don't have a pile of notes on them anyway - it's simply that I'd much rather not go through that pile of notes again, if at all possible, thank you. To unload though for now, the names I'd mention at all are quite few anyway and go in a rather obvious order from the fundamentals to petering out on the edges: there's Blum's medial axis (1967); there's Bloomenthal's work on skeletal design of natural forms (1995), including the algorithm I'm using so far; there's Shewchuck's work -starting with his thesis (1995) and building up from there- on Delauney refinements for mesh generation and his useful lecture notes at least; there's Persson's thesis (1997) on mesh generation from implicit geometries, which includes the attempt at mesh generation based on a truss-model; there's a readable book by Edelsbrunner from 2001 on Geometry and Topology for Mesh Generation; there's perhaps some of the earlier work (2001 and earlier) by Amenta on approximating a surface ("power crust") based on the medial axis transform and a union of balls - effectively an approximation of the medial axis itself. I've added the years for a reason but by now I'm quite satisfied I have obtained a reasonable map of the domain both in names and in time coordinates really - if you want something usable and useful as opposed to something big, unyielding, overly complex and utterly narrow in its application, your destination has to be the '90s at the very latest. ↩
"An Implicit Surface Polygonizer", Jules Bloomenthal ↩
If the surface is bounded - like a torus say, this is obvious enough. If the surface is unbounded, then the "whole surface" is simply defined based on a bounds parameter provided as the maximum number of cubes to explore in each direction from the starting point. Simple, effective and to the point, it's as if the author actually wanted to make something truly useful, you know? ↩
There is of course also the fact that any run will polygonize a connected surface ie not disconnected parts but I don't quite see this as any sort of limitation really - wtf is that "disconnected surface" anyway, if it's disconnected then it's made of 2 parts and if it's made of 2 parts then each part can be treated as one surface and look that there's no problem anymore and we can actually get something done instead. ↩
By now, I almost have a sneaking suspicion that if I ever get to actually play Eulora myself as opposed to programming its server and its client and its graphics and ~everything else, I'll play it in awk already. ↩
And I can't look at that thing without instantly hearing this song of Ioan Gyuri Pascu:
Mi-au zis baietii:
Vezi ca fata asta-i
Un element inabordabil
N-ajungi la ea, oricate precautii
ti-ai lua in prealabil
si eu, care nici macar
Sa inot nu stiu
Ce sa fac?
Pentru un prim pas
Musai sa-mi cumpar un colac.Mi l-am si cumparat
Cu grija l-am umflat
Usor in apa am intrat
Si mandru am cantatHei tu, mi-am luat colac
Sa vezi acuma cum devine marea un fleac
Hei tu, mi-am luat colac
Sa vezi acuma cum devine marea un fleacScena de film:
Eu daruindu-i cu amor
O stea de mare.
Si m-am trezit
Cu masca de oxigen
Pe fata, la reanimare
Ea, doctor in halat
Cu o seringa imensa in mana
Mi-a zis: halal colac baiete
Noroc cu medicina romana!Acum ca te-am salvat, mi-a zis:
Mai canta-mi inc-o dat’
Refrenul acela minunat.
Normal ca l-am cantat.Hei tu, mi-am luat colac
Sa vezi acuma cum devine marea un fleac.I-am zis: stiti domnisoara
La un moment dat
Credeam ca
M-am inecat in mare
Habar n-aveam ca aveti
O privire asa cuprinzatoare.
Mi-a zis: hai lasa textele
Galanteria nu-i intotdeauna un atu.
Mai bine ofera-mi floarea de pe masa
Ia-ma de brat si spune-mi tu.Si brusc m-a sarutat
Apoi s-a maritat,
Bineinteles, cu alt baiat.
De fapt, am inventat.Nimic, nimic din ce v-am cantat
Nu are baza
Desi, desi tare, tare
M-as fi bucurat.Ma rog, asta-i muzica,
Frumoase lucruri
Regaseste omul in ea
Da, da, da’ ce frumoasa-i muzica
Mai ales cand omul regaseste
Atat de multe lucruri utile, educative,
Frumoase si morale in ea, vai!Nimic, da’ nimic, nimic
Din ce v-am cantat
Nu are baza
Desi tare, tare
Si va spun, pe cuvantul meu
M-as fi bucurat.Ma rog, asta-i muzica
Pe cuvant, atat de inaltatoare
Lucruri gaseste omul in ea
Va spui, eu, vai de mine…
Asa-i de frumoasa
Si de educativa...
Comments feed: RSS 2.0


Moving right along.
Well, pushed, pulled, kicked, somehow it has to move and certainly right along :D
Thanks!