Forced by the blunt but all mighty forces of necessity, I've spent most of the past month reading a bit more on the Maths underpinning all cryptography and otherwise digging deep into the guts of the miserable-but-we-don't-have-any-better Gnu Privacy Guard 10. The goal of this yet another stable cleaning was to extract from the shit pile only those parts (very small by comparison to the whole) that are at all ...useful. Useful of sorts and of the rather poor and broken sorts, of course, but when necessity bites, there is no choice anymore and any sorts will simply have to do. It is what it is and its name at the end of the day is simply being poor so I don't care what money, tits and anything else you've got but if you have no choice than to use broken stuff and shitty pieces then you are still poor and nothing else.

On the brighter side, this time a big chunk of the work had been already done in the shape of the sane-mpi package expertly and very, very helpfully carved out of the insanity by Stanislav Datskovskiy. The man did many other useful things too -a true source of randomness for computers included- but I clearly owe him at least a meal for this if nothing else.

Getting straight to the business, the most tangible result of some of the work done this month is an incipient RSAtron conforming as much as possible at the moment with the current TMSR-RSA specification. The sane-mpi package is used as it was provided and linked as a library. In addition, I extracted and adapted basic key generation, encryption and decryption (for now, encryption and decryption are provided as direct application of public/private keys without any padding or anything else - this is just the first step). The keys itself are simply stored as structures of relevant MPIs, as the whole RFC4880 mess is set to be supplanted by some saner spec. As a first step and for testing purposes only, I have also a very basic read/write keys from/to file simply as hex.

It's worth noting that one of the more gnarly parts that I had to extract was key generation simply because existing key generation in GPG does a lot of dancing about the plain fact that no, it does not use a true random generator no matter how much it avoids saying so plainly. So I kept then the approach (get chunks of random bits of desired size until you find one that is a prime number) and the existing primality test (Miller-Rabin for lack of a better one) but I changed the whole thing so that it actually uses as input true random bits obtained directly from a Fuckgoats connected to the machine. I also changed the number of M-R iterations¹ from 5 to 12, more on the principle of "why not" than on any claim that this achieves some degree of security. For concrete numbers, the error probability for M-R when *actually using true random integers for testing* is upper bounded by 0.25^12 when using 12 iterations and that's 0.00000006. In other words, the probability that the Miller-Rabin test wrongly returns "prime" on a non-prime number when using 12 iterations is less than 0.00000006.

As per TMSR RSA specification, size of key is set to 4096 bits (hence, two primes of 2048 bits each). Note that all key pairs at the moment have same public exponent as GPG-generated keys have.

Once this very first step of a working RSA-tron was completed, I ran a few tests to get some concrete numbers regarding the CPU time eaten by RSA operations with this setup. All tests are run on a rather modest i5 CPU 3.2GHz under Ubuntu 14.04, 64 bits. Durations are given as CPU time in seconds, as reported by the clock() function (time.h) and calculated as ( (double) (end - start) ) / CLOCKS_PER_SEC where start is the value returned by clock() right before starting the RSA operation and end() is the value returned by clock() right after returning from the RSA operation. Here are the main results:

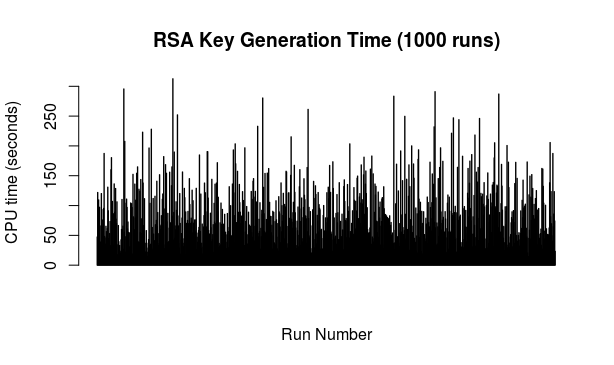
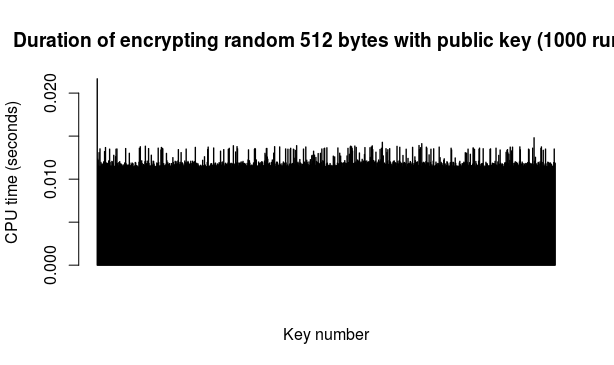
Key generation: the testing script was set to generate 1000 keys of 4096 bits each. Only the key generation was timed each time but the script did afterwards actually check each key and moreover spit them out into a file for further use. All in all, this part took a bit less than 24 hours. Here's the picture of time (in seconds) taken to generate each of those 1000 keys in the order in which they were generated (M-R with 12 iterations):

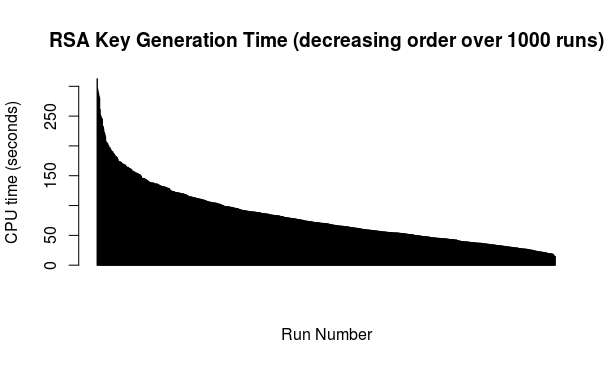
To my eye the above looks nicely lacking any clear pattern but in any case, there are obvious spikes when one could presume longer spells of non-prime random candidates, occasional dips and loads of cases in between. For the curious, here is the above ordered from longest time to shortest time:

Encryption/decryption: a run of this test simply took 512 random bytes (from Fuckgoats) as "message" and then proceeded to encrypt it with the public key from each of the 1000 key pairs followed by decrypting the result with the corresponding private key. The 512 figure is chosen because it is the current S.MG (Eulora) length of a packet. The encryption and decryption operations were timed separately.

Here are the results of 2 runs of this test (so 2 different "messages" encrypted and decrypted with each of the 1000 keys in turn):

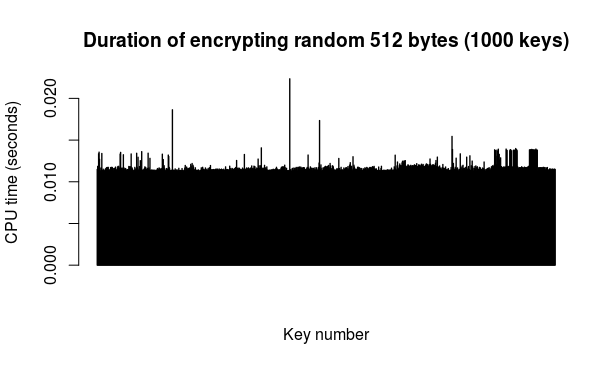
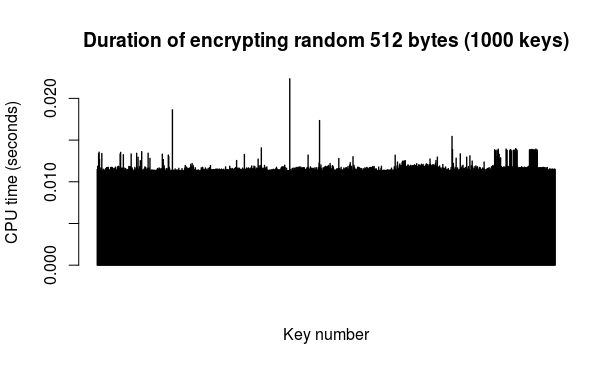The above 2 runs put together on the same plot for convenience (one run after the other).

And all the above durations (2000 total) put together and ordered from highest to lowest for encryption and decryption, respectively:

As durations are indeed and as expected rather similar, an overall average makes some sense. Based on the above data, the average encryption time is 0.0112 seconds per 512 bytes, while the average decryption time is 1.1082 seconds per 512 bytes.

For the curious and for whatever it is worth (not much): the average duration of key generation from the above data works out as 80.712 seconds so about one minute and a half.

And here are the data files behind the above plots and numbers:

1. key generation durations (1000 keys, M-R 12 iterations)
2. key use first run
3. key use second run

---

1. or "security parameter" according to the Miller-Rabin test description on page 139 of Menezes, A. J., van Oorschot, P. C. and Vanstone, S. A., "Handbook of Applied Cryptography", CRC Press, 1997 ↩

Category: Coding

Comments feed: RSS 2.0