The 2020 end of year fractals come in frame shape and biscuit flavour - as far as I can tell, quite possibly as a payback for that time when I plainly sad I'll have fully transparent windows rather than live with those horribly boring "artistic" borders that the legacy client came with. So now I'm making a full series of ornate borders essentially and at this rate, I can see it ending up with me *wanting* to add borders to windows too, for crying out loud. In any case, have a look at fractals on the border or otherwise biscuit design to render the chef insane with envy:

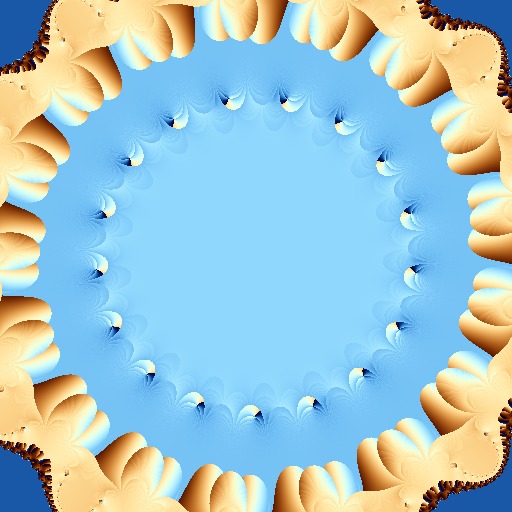
To obtain such ornate borders, I changed just one important thing in those high order complex polynomials of last time, essentially aiming at first to explore a bit the Julia set as well, since anyway, Monsieur Julia got less press than Mandelbrot: instead of iterating from the origin and using each point of the texture space as offset (ie as free term), this series iterates from each texture point directly and uses an MT-value (hence, seed-dependent) as offset. To keep it clean, tidy and ultra-regular as you might have noticed already, this series sticks also to the default definition of Julia-like fractals in that all polynomials are simply z^n + c (ie the coefficient of z^n is 1, the free term is c and all the other coefficients are 0).

On the very convenient side of this new series, it turns out that my previous choices of positioning in the complex space and even other parameters work perfectly well for this series too. As a result, I had only to add one single additional switch to my generator to get it to churn out (and fast, one great advantage of those series are that they are *very* fast, especially compared to the noise-based series, perhaps one day I'll find the time to write about this, too) a whole pile of them - the images included above are just a selection. Moreover, the degree of the polynomial can vary a bit too around that same 20 value used otherwise - it's this relatively high degree that gives the round shape and pattern, as noticed previously, but changing it slightly (+/- 5 at most) works too.

On the downside of this new series, the approach is essentially less stable than my previous one (and that's why I went first with that rather than with this) - some seeds can make for lousy offsets that end up in some cases as just nothing at all (well, a plain, single colour, filled rectangle, arguably not exactly nothing at all but close enough). Perhaps this can be avoided by adjusting the interval for those offsets - currently I have no idea if there is an interval in which *all* values make for some sort of pattern at least. For the easy approach, I just went with what I had so that the offsets are picked in the interval -1.5 to 1.5 (there is some interplay with the rest of parameters, hence it's not that surprising that those work for this series since they worked for the previous one, too). Anyways, if there will be further exploration of this series, perhaps this interval is one of the parameters to look at, too. Before that though, there are certainly quite a few *other* directions I'd rather explore...

And before you ask, otherwise, the above are just part of my still-growing list of stuff to write up, since - most naively - I tried to apply the end of year tidy up approach to fractal matters. In hindsight, I should have known better what will come out of "write-ups" at this time of the year - why, even more to write about than before doing the write-up, what else?¹ Oh well, there's a whole new year ahead - one for ever more write-ups, why not!

Happy New Year!

1. Also a ton of images, so that I finally realised that the stupid Image Viewer thing is so idiotically made as to *preload* all images in a directory before it shows anything - as a result, hanging mightily when confronted with the fresh output of my image generator. Oh well, long live feh I suppose, yet again. ↩

Category: Coding, Computer Graphics

Comments feed: RSS 2.0